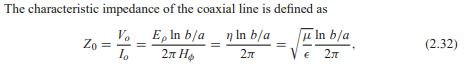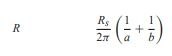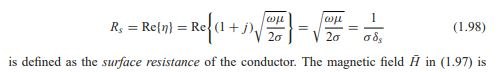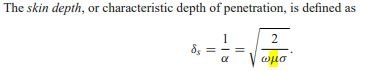Comments
-
wire and coax impedanceLate to the topic but a good source for this is Pozar 4th Ed. Eq. 2.32.
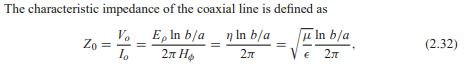
In regards to Z= Zo x sqrt(mu_r/epsilon_r), I don't think so? Especially since the question regarded additional R (hence the conductors mu) but impedance formula uses medium mu. For what it's worth, in above, sqrt(mu/epsilon) = sqrt(mu_0 * mu_r/(espilon_0 * epsilon_r). Generally for coax impedance equations you see mu_r is assumed unity and the free space constants are evaluated out, so only sqrt(epsilon_r) is left in the denominator as a variable. So, if the mu_r of the medium happens to be non unity, the impedance should change by a factor of sqrt(mu_r).
Now for where conductor mu plays a role, of course Z0=sqrt( (R+jwL)/(G+jwC) )
For coax:
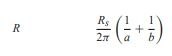
Where:
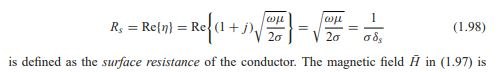
and finally we see conductor mu in skin depth:
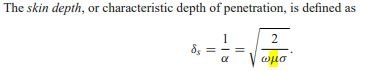
Dillan

Start FollowingSend a Message
- Terms of Service
- Useful Hints and Tips
- Sign In
- © 2026 Microwaves 101 Discussion Board